Hands-on: X25519 Key Exchange
Let's exchange a secret to start a secure conversation.
Overview
Key exchange is a mechanism where two parties (Alice and Bob) can agree on the same number without an eavesdropper being able to tell what it is. X25519 is the name of one method of key exchange, by doing point operations on the Curve25519 elliptic curve:
With those point operations, we'll be doing a key exchange that looks like this:
Let's give the above terms some better names:
| ka | : | Alice's secret key - a 256-bit (32-byte) random number |
| kb | : | Bob's secret key - a 256-bit (32-byte) random number |
| P | : | a point on the curve, where x=9 |
| ka∗P | : | Alice's public key |
| kb∗P | : | Bob's public key |
| ka∗kb∗P | : | The shared secret |
Math on the curve
This section can be skipped, it just gives a flavor of the math of elliptic curves. An in-depth animated explanation for this section can be found on a sister page.
Point operations (performed on points on the curve):
- Adding two points on the curve gives a third point, based on the line between two points and its intersection with the curve.
- Repeated additions of a point on the curve gives us scalar
multiplication:
2P=P+P
3P=P+P+P
6P=P+P+P+P+P+P
... etc. - Adding points on the curve is associative: adding
the results of point addition will give the same result
as adding the component points individually:
P+P+P+P = 3P+P = 2P+2P = 4P
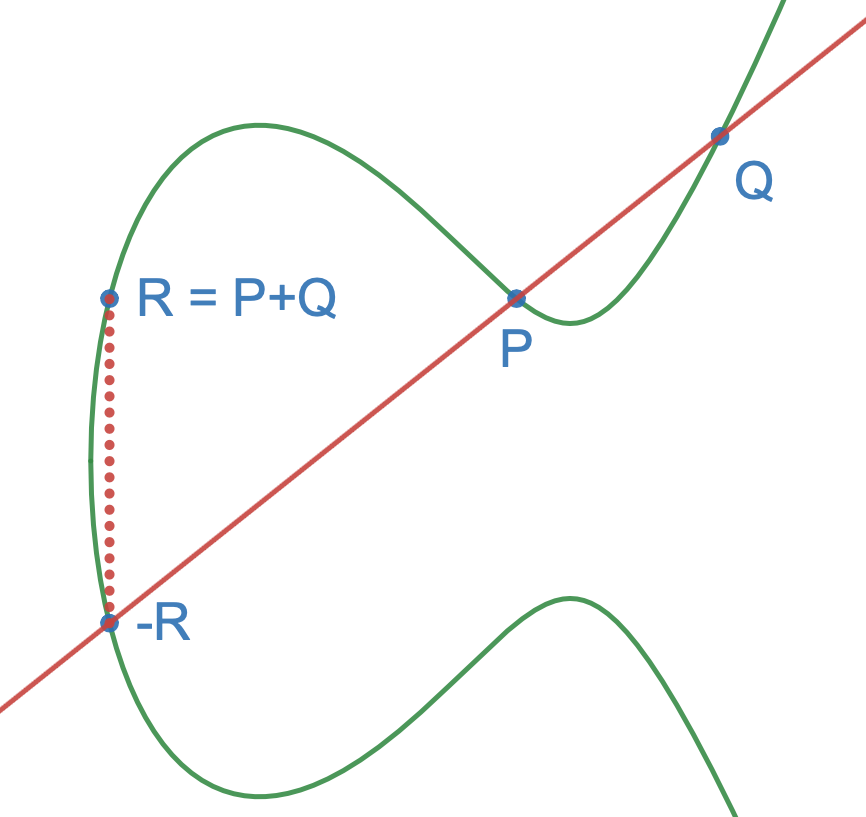
Point Addition: P+Q=R
Modular arithmetic (used when calculating addition and multiplication of points above):
- Adding, subtracting, and multiplying numbers will "wrap around" at the prime p=2255-19.
- Division is replaced with the multiplicative inverse: instead of dividing by x we find the number x-1 that satisfies the relationship x∗x-1 =1 in our prime field, and multiply by that.
→ 7∗10mod23=1; 7-1 = 10
→ 4∗10mod23 = 17
Hands on
Let's play with some actual numbers. This calculator lets us do scalar multiplication on the base point P, which is a point on the curve with coordinate x=9. These calculations only give the x coordinate of nP, the y coordinate is not needed or used.
Let's perform a simple key exchange. Give Alice a secret key, such as "7", and use the calculator above to find Alice's public key. Give Bob a different secret key, such as "5", and use the calculator to find Bob's public key:
- Alice's secret key: ka = 7
- Alice's public key: kaP (7P) = 0daf32e7ed8099122b2dfa4c1d8c4a20c0972a1538bf0575338aae0fe0841828
- Bob's secret key: kb = 5
- Bob's public key: kbP (5P) = 41b6ec3c50ee7af203c0026e5e079e7fa8cbc9bc581d49cb0d537d5778497c87
Now let's be Alice. Put Alice's secret key (ka) into the calculator below, and use it to multiply Bob's public key (kbP).
- Shared secret: kakbP (35P) = 1b9b715c415e547a13ca98a9f561d54499cc7402a1098414eddcfaf83ffbe3f8
Let's switch over to Bob. Put Bob's secret key (kb) into the calculator, and use it to multiply Alice's public key (kaP). The result matches, because kakbP = kbkaP = 35P.
Since the eavesdropper can't see either of Alice or Bob's secret keys, they can't compute the same result.
Odds and ends
Q: What is the key strength of X25519?
A: The key size of X25519 is 256 bits (32 bytes), but five of those bits are "clamped" to fixed values to address various security concerns:
| Bits | Value | Reason |
|---|---|---|
| 0,1,2 | 0 | Protect against small-subgroup attacks, which would allow one peer to use a manipulated secret key to discover the other peer's secret key |
| 254 | 1 | Prevent implementors from skipping a multiplication round for smaller keys, which would expose a timing leak |
| 255 | 0 | Constrain n < 2255, which prevents the algorithm from reaching the "infinity" result for base-point x=9 |
Q: Why can't I reproduce
these results in
A: Private keys used in actual X25519 exchanges are modified slightly (see "Clamping" above), and you'll need to set/clear the same five bits yourself on any keys that you use for key exchange.
You may still find that your output does not match because X25519 keys are stored and transmitted in little-endian order while this page displays them as plain numbers. Flipping the byte order should match them up.
Q: If these are points in an x-y curve, where are the y coordinates?
A: The y coordinates for each point are not needed for X25519, and for simplicity they are not computed. Using only the x coordinate also reduces public key length, as the y coordinate isn't part of the key.
Each valid point on the curve has two y values that satisfy sqrt(y2).
Only half of x values are valid on Curve25519. Going back to our curve equation, valid means that the expression x3 + 486662x2 + x results in a number that in modular arithmetic has a square root (to satisfy the y2 side of the equation).
Q: What does Curve25519 look like?
A: Here's what the curve looks like in real numbers,
(i.e. floating point numbers with standard addition and multiplication):
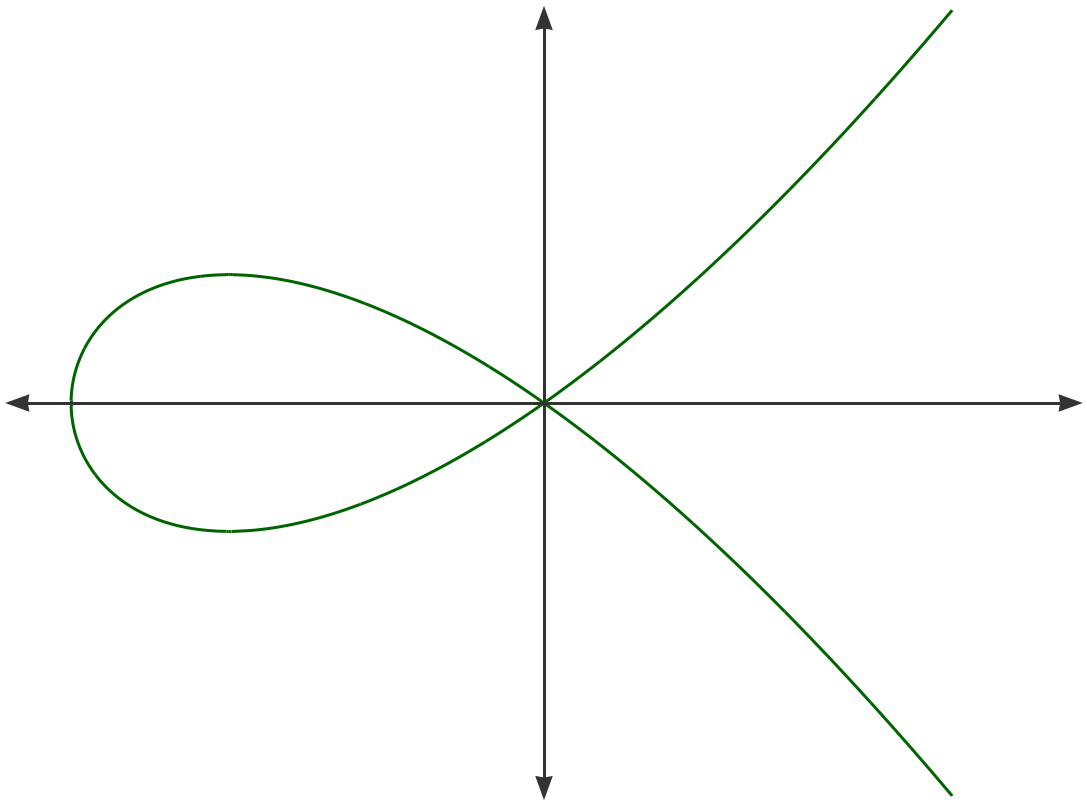
y2 = x3 + 486662x2 + x
And here's the first points of the curve when calculated in 𝔽p (i.e. with integers 0..2255-19 using modular math):
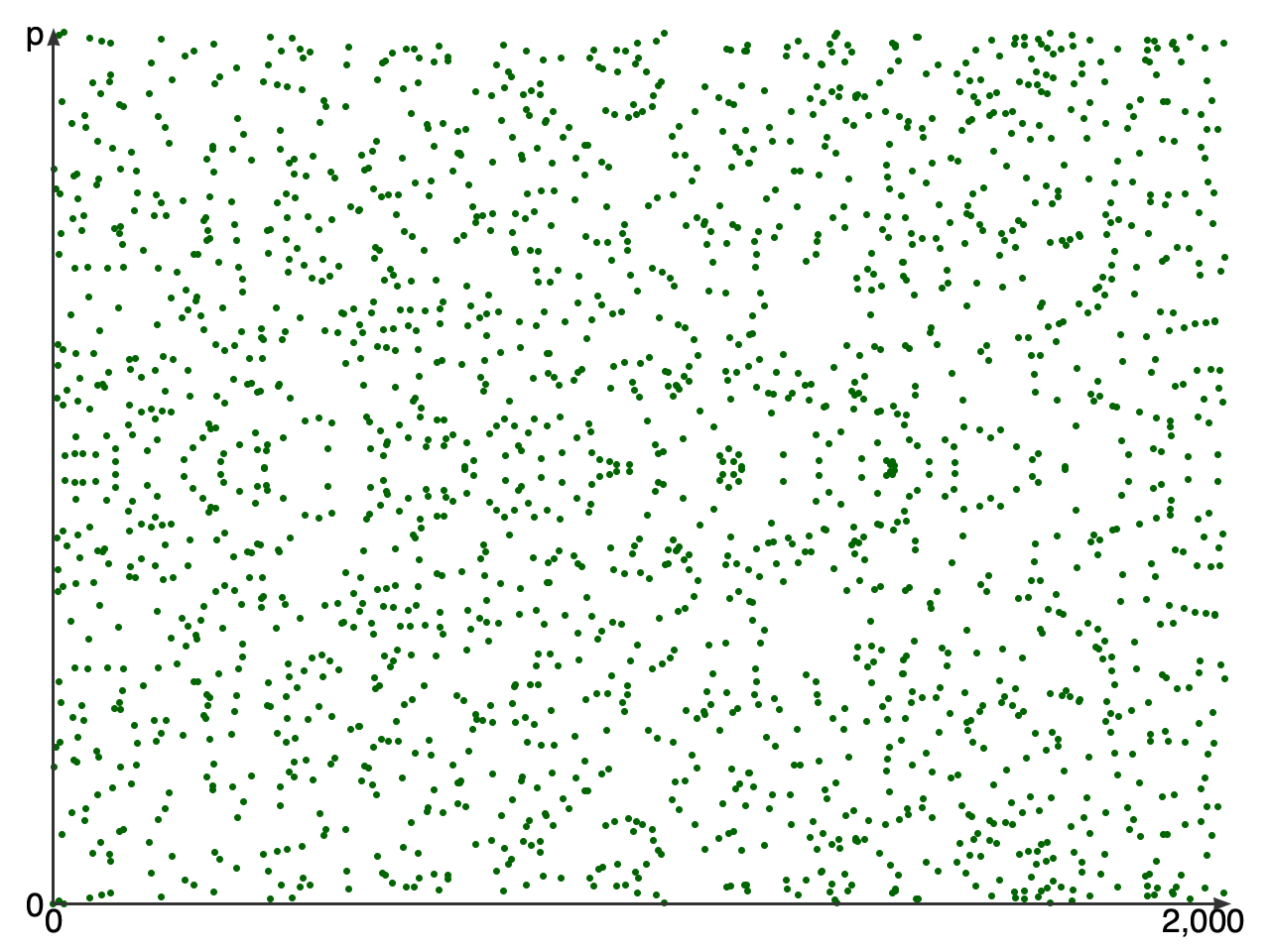
y2 = x3 + 486662x2 + x in 𝔽p
Q: Can you give me more details on elliptic curve operations?
A: I found the following useful:
- Curve25519: new Diffie-Hellman speed records - explains the curve and how it was derived
- The Animated Elliptic Curve - an animated exploration of the concepts behind EC cryptography
- Wikipedia: EC point multiplication - particularly the section on Montgomery ladders
- Wikipedia: Montgomery arithmetic - includes equations for addition and doubling of points
- RFC 7748 - recommended algorithm for X25519 multiplication in constant time with a Montgomery ladder
- PDF: Implementing Curve25519/X25519 - as noted above
- Elliptic Curve Cryptography: a gentle introduction
The code for this project can be found on GitHub.